Experiments
To evaluate the results of our implementation, we compared them with the results of RarestFirst algorithm. We use a set of two metrics. The first metric is the diameter of the team, that is the longest shortest path between any two nodes in the team. The second one is the sum of weights (SW), that is the sum of the weights of the edges of the team's subgraph. In the following figures we show the result of our modified RarestFirst implementation and original RarestFirst in terms of the diameter and SW on the best team on the Epinions' dataset.
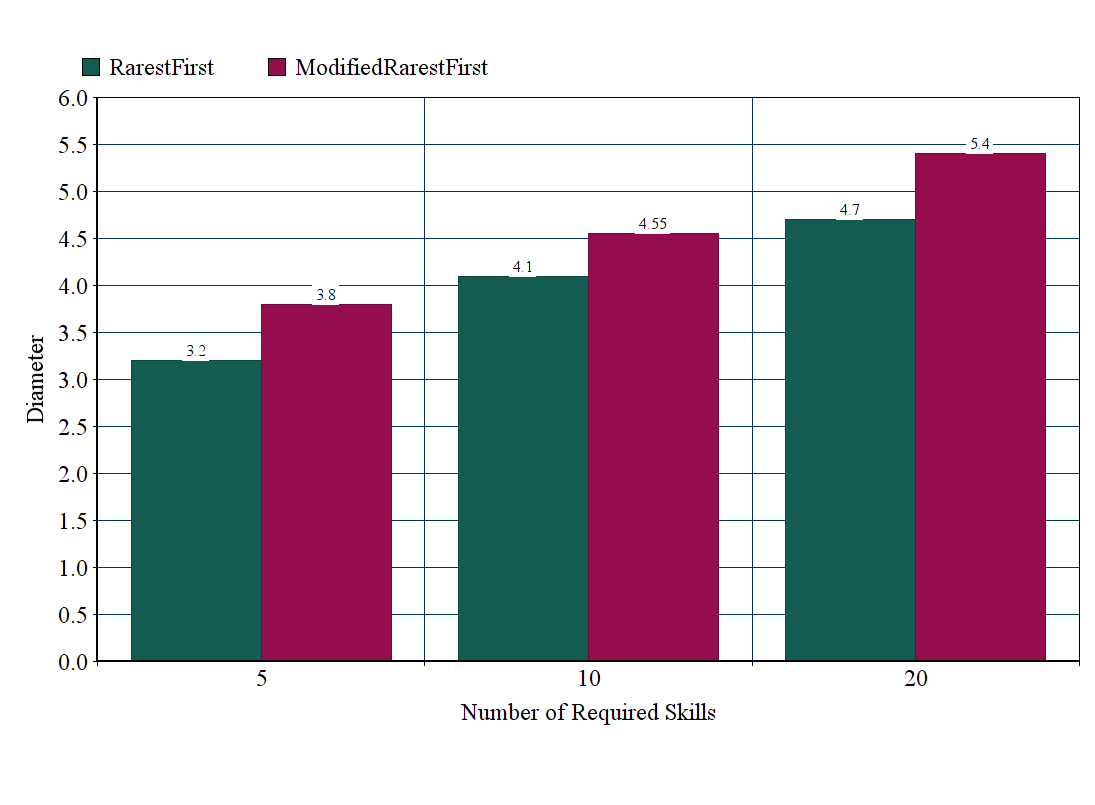
Comparison of modified RarestFirst and RarestFirst using diameter as performance metric.
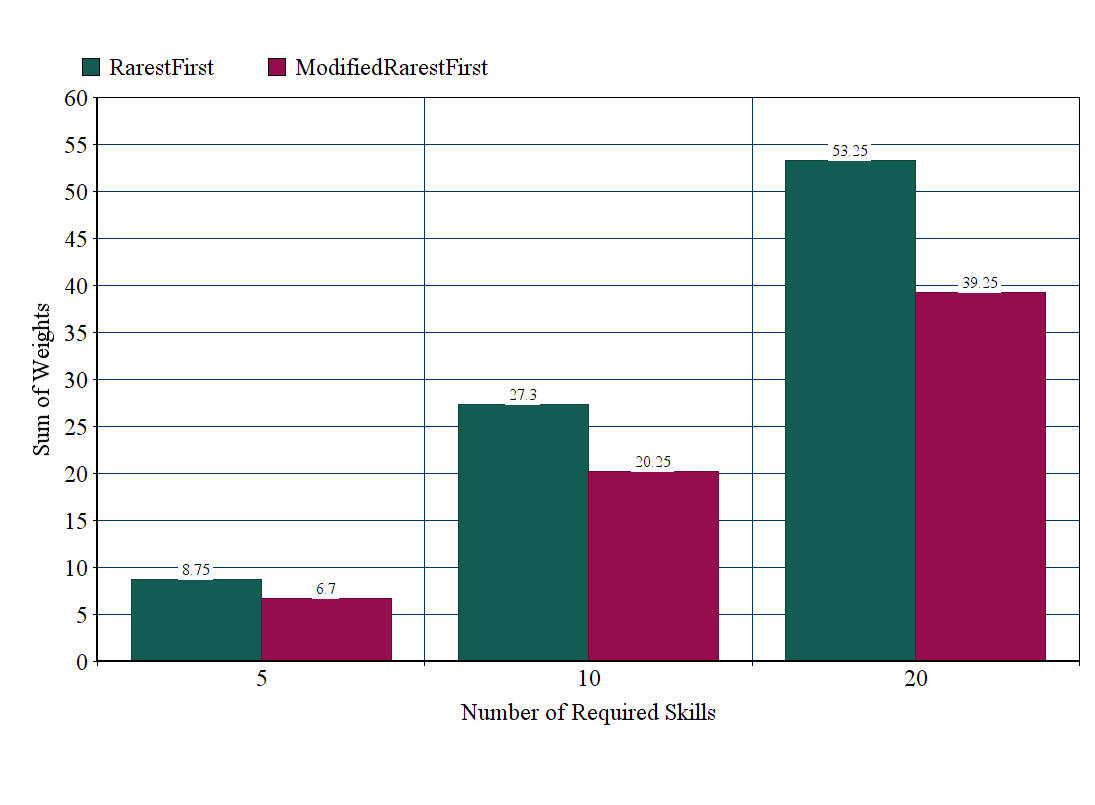
Comparison of modified RarestFirst and RarestFirst using sw as performance metric.
Our main goal was to produce teams with small communication cost, that have as less negative links as possible. In order to achieve this goal we had to sacrifice the diameter cost of the team, to avoid a negative link. Smaller diameter doesn't mean a better result in a network with negative edges, as it measures the cost between the two experts that are furthest away from each other, and does not measure the cost of all the required communication. A team with a negative link may have a smaller diameter than one with no negative links.
The following figures show an example of a best team produced with RarestFirst algorithm and a best team produced with our modified RarestFirst algorithm
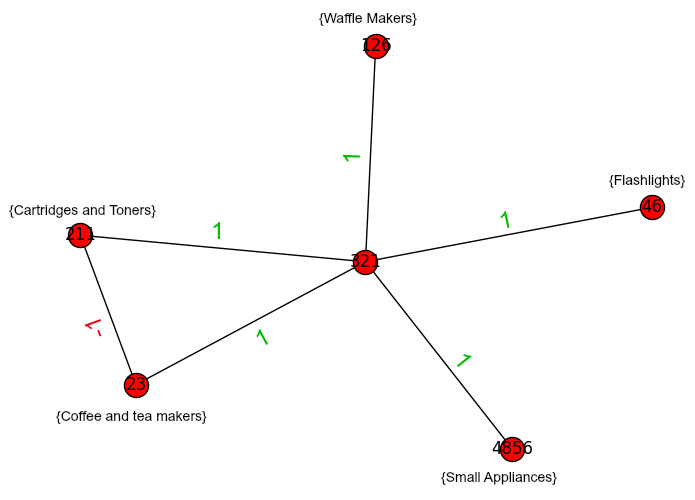
Subgraph of team produced with RarestFirst algorithm for project P={Coffee and Tea Makers, Waffle Makers, Small Appliances, Cartridges and Toners, Flashlights}.
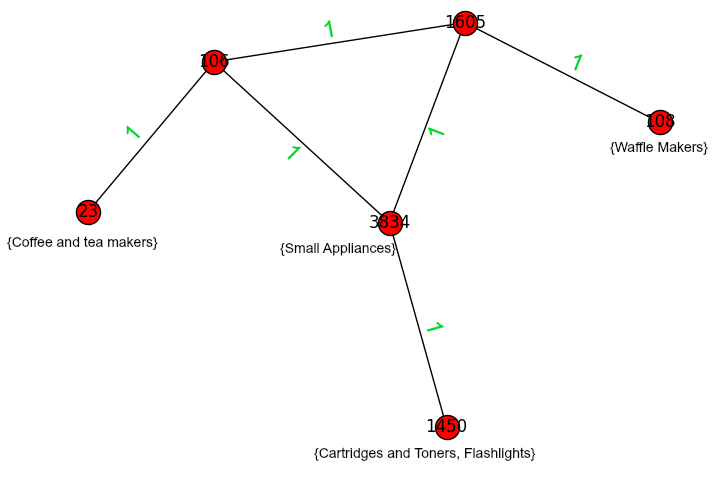
Subgraph of team produced with modified RarestFirst algorithm for project P={Coffee and Tea Makers, Waffle Makers, Small Appliances, Cartridges and Toners, Flashlights}.
In the figures above we have a random project P={Coffee and Tea Makers, Waffle Makers, Small Appliances, Cartridges and Toners, Flashlights} as an example. The numbers on the edges represent the label -1 for negative links and 1 for positive. A negative link in our graph has a weight higher than the diameter of G (10), while a positive has weight 1. RarestFirst algorithm gives as best team the graph of figure 4. This team has diameter value 2 and SW value 15, since it contains a negative labeled edge. Modified RarestFirst gives figure 5 as the best team. This team has diameter 3 and SW value 6. This is an example of a case that smaller diameter is not preferred, as there is a better solution with no negative links and with slightly bigger diameter available.